'''
구성은
1. 문제 설명
2. 원본 문제(코드)
3. 강사 답안
4. 주최측 답안
순으로 되어있습니다.
빈칸채우기와 한 줄 수정의 경우
강사 답안과 주최 답안이 유사 / 동일할 수 있습니다.
#문제5
다음과 같이 n x n 크기의 격자에 1부터 n x n까지의 수가 하나씩 있습니다.

이때 수가 다음과 같은 순서로 배치되어있다면 이것을 n-소용돌이 수라고 부릅니다.
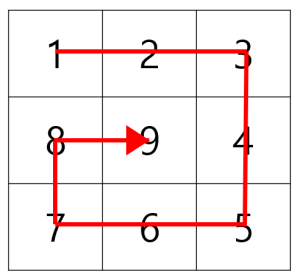
소용돌이 수에서 1행 1열부터 n 행 n 열까지 대각선상에 존재하는 수들의 합을 구해야 합니다.
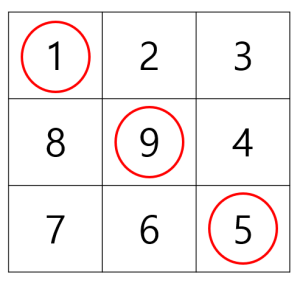
위의 예에서 대각선상에 존재하는 수의 합은 15입니다.
격자의 크기 n이 주어질 때 n-소용돌이 수의 대각선상에 존재하는 수들의 합을 return 하도록 solution 함수를 완성해주세요.
---
##### 매개변수 설명
격자의 크기 n이 solution 함수의 매개변수로 주어집니다.
* n은 1 이상 100 이하의 자연수입니다.
---
##### return 값 설명
n-소용돌이 수의 대각선상에 존재하는 수들의 합을 return 해주세요.
---
##### 예시
| n | return |
|--- |-------- |
| 3 | 15 |
| 2 | 4 |
##### 예시 설명
예시 #1
문제의 예와 같습니다.
예시 #2
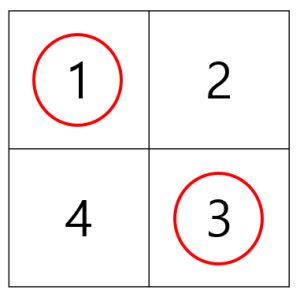
1과 3을 더하여 4가 됩니다.
#You may use import as below.
#import math
def solution(n):
# Write code here.
answer = 0
return answer
#The following is code to output testcase.
n1 = 3
ret1 = solution(n1)
#Press Run button to receive output.
print("Solution: return value of the function is", ret1, ".")
n2 = 2
ret2 = solution(n2)
#Press Run button to receive output.
print("Solution: return value of the function is", ret2, ".")
'''
#You may use import as below.
#import math
def solution(n):
answer = 0
ori = 0
for i in range(n):
# 오른쪽 위 꼭지점 양 옆 변 부분과 왼쪽 아래 꼭지점 양 옆 변 부분을 반복하며
# 점점 중간으로 나아가는 for 문입니다.
start, end = ori + 1, ori + 2 * (n - i) - 1
# start와 end는 꼭지점 양 옆 변에서 가장 작은 수와 가장 큰 수 입니다.
if i % 2 == 0:
# 대각선 성분이 존재하는 곳은 i가 0, 2, 4, ...로 짝수일 때 입니다.
if end < n ** 2: answer = answer + start + end
# 대각선 성분 중 가장 큰 값이 판에서 가장 큰 수보다 작은 경우
# start와 end가 전부 유효하므로 더해줍니다.
elif start == end: answer = answer + start
# n이 짝수인 경우 상관이 없지만 홀수인 경우에는
# 정 중앙의 값이 생기는데 이는 start와 end가 같은 경우입니다.
# 따라서 이 경우에는 start와 end중 하나만 더해줍니다.
ori = end
# 오른쪽 위와 왼쪽 아래 꼭지점이 바뀔 때마다 시작지점인 ori를 업데이트합니다.
return answer
#The following is code to output testcase.
n1 = 3
ret1 = solution(n1)
#Press Run button to receive output.
print("Solution: return value of the function is", ret1, ".")
n2 = 2
ret2 = solution(n2)
#Press Run button to receive output.
print("Solution: return value of the function is", ret2, ".")
'''
주최 제공답안
def in_range(i, j, n):
return 0 <= i and i < n and 0 <= j and j < n
def solution(n):
pane = [[0 for j in range(n)] for i in range(n)]
dy = [0, 1, 0, -1]
dx = [1, 0, -1, 0]
ci, cj = 0, 0
num = 1
while in_range(ci, cj, n) and pane[ci][cj] == 0:
for k in range(4):
if not in_range(ci, cj, n) or pane[ci][cj] != 0:
break
while True:
pane[ci][cj] = num
num += 1
ni = ci + dy[k]
nj = cj + dx[k]
if not in_range(ni, nj, n) or pane[ni][nj] != 0:
ci += dy[(k + 1) % 4]
cj += dx[(k + 1) % 4]
break
ci = ni
cj = nj
ans = 0
for i in range(n):
ans += pane[i][i]
return ans
'''