이 글의 대상 독자는 두 부류다.
1. 고사양 컴퓨터를 구매하였는데 고작 파스 점수나 게임 프레임 숫자 약간의 차이 이상을 원하는 '합리적 소비자'
2. 비록 저사양이거나 오래된 동료와 같은 컴퓨터이지만 혹시나 하는 '내가 몰랐던 다른 모습' 을 발견하고자 하는 자.
예를들어 이백만원 주고 산 A군은 백만원짜리보다 더 압도적인 힘을 원함에도 불구하고
컴퓨터를 '굴리는' 방법을 잘 몰랐기 때문에 최대성능을 뽑아내기 어려웠다.
고작 실행시간 1~2초 차이? 받아들일 수 없다.
그렇다면 적어도 파이썬 코딩에서만큼은 스펙이나 벤치마크 점수 이상의 '무언가' 를 체감할 수 있는 방법은 없을까?
답은 '있다' 이다.
파이썬은 기본적으로 1스레드를 사용한다.
이게 무슨 말이고 하니 ctrl + alt + del 을 눌러 작업관리자에 들어가보자.
오른쪽 아래에 논리 프로세서라는 놈이 보일텐데, 부품마다 다르겠지만 보통 4에서 많으면 24나 36까지 있다.
아래 예시에는 12로 되어있다.

그러니깐 일꾼이 12명 있는데 파이썬은 기본적으로 그 중 한명하고만 작업한다 이 말이다.
100%를 12로 나누기하면 8퍼센트 정도인데 지금은 4%니까 현재 이 놈은 1인분 일도 안 하고 있다는 얘기다.
파이썬으로 뭘 돌리면 여러분들은 어지간하면 20%도 넘지 못할텐데 라이브러리의 힘으로 올리는 경우도 있지만
데이터 핸들링할때는 응 그런거 없기 때문에 직접 작업을 만들어서 할당하는 방식으로 사용해야 한다.
for문 같은거 돌려놓고 한참 기다리는 와중에 작업 관리자 켜보니까 CPU 점유율이 10%도 안된다?
12명이 할 수 있는거 1명만 하고 있으면서 열일하는 척 하는 것이다.
이 글은 이런 꼴을 안 보기 위함이다.
컴퓨터를 '올바로' 사용하기 위한 예시로 수학문제를 하나 가져왔다.
콜라츠 추측이란?
한 숫자를 고르고 이를 x 라 하자.
x에 대해
홀수이면 3을 곱하고 1을 더한다.
짝수이면 2로 나누기 한다.
모든 수에 대해(양수 한정) 위 과정을 홀수/짝수를 판별하여 계속 이어나가면 결국 1이 될 것이라는 추측이다.
만약 5를 골랐다면 홀수이기 때문에 3을 곱하고 1을 더하여 16이 되고
16은 짝수이므로 2로 나누기하여 8이 된다.
8도 짝수이므로 2로 나누어 4가 되고
4도 짝수이니 2로 나누어 2가 되고
결국 2 나누기 2 하여 1이 된다.
5 -> 16 -> 8 -> 4 -> 2 -> 1 인 것이다.
...
만약 9를 골랐다면 위 과정이 20단계나 되어서 손으로는 약간의 노오력이 필요한 정도가 된다.
포괄임금 무보수로도 불평불만 없는 파이썬이 필요한 때가 되었다.
1 부터 100만까지의 모든 숫자에 대해 콜라츠 추측으로 수열을 만들어 데이터 프레임으로 만들어 볼 것이다.
위 예시에서 5는 직접 해봤지만 세상에 숫자는 많고 인력은 귀하기 때문에 사람 대신 파이썬을 이용하여 일을 시킨다.
일단 사용할 도구들을 불러온다.
계산량이 많으면서 숫자간 상호 의존성이 없기 때문에 병렬처리가 가능하다.
따라서 멀티프로세싱으로 CPU 점유율을 100% 활용해 주도록 하자.
22세기 노예 ON
import matplotlib.pyplot as plt
import pandas as pd
from coll import col, num_ext
import multiprocessing as mp
pool = mp.Pool(32)
위 coll 에 들어있는 함수 col 이다.
숫자를 하나 집어넣으면 콜라츠 추측에 해당하는 수열을 뽑아줄 함수를 만들었다.
이제 col(10) 하면 10이라는 숫자에 대해 수열을 뽑아줄 것이다.
수열 뿐 아니라 몇 번의 과정을 거쳐 1이 되는지와 최대 몇까지 커졌다가 내려오는지 확인하는 정보를 넣었다.
def col(i):
dt = {str(i) : []}
j = i
while True:
if j == 1:
dt[str(i)].append(j)
return {'init' : i, 'max' : max(dt[str(i)]), 'count' : len(dt[str(i)]), 'series' : dt[str(i)]}
elif j % 2 == 0:
dt[str(i)].append(j)
j = int(j / 2)
else:
dt[str(i)].append(j)
j = 3 * j + 1
위 함수를 멀티프로세싱하여 노가다시킨다.
1 부터 백만까지 숫자를 리스트로 만들어 col 함수에 집어넣는 작업을 32개의 업무로 나누어 분배한다.
for_df = pool.map(col, [i+1 for i in range(int(1e+6))])
df = pd.DataFrame(for_df)
df 변수에는 시작 숫자인 init, 얼마까지 찍고 내려왔느냐는 max, 몇 단계를 거쳐 1로 돌아왔는지의 count와
마지막으로 콜라츠 추측에 해당하는 수열인 series 컬럼으로 데이터가 잘 모셔져 있다.
그리고 오른쪽은 이를 수행하기 위해 사용된 컴퓨터의 CPU 점유율이다.
일꾼이 12명인데 업무가 32개이니 놀면서 할 여유따윈 없을 것이다.
그 증거로 EZ하게 점유율 100%를 채웠지 않은가?

이왕 이렇게 된거 '수학' 스러운것을 하나 해보자.
수열에 나오는 숫자들이 숫자 몇으로 시작하는가? 0 부터 9 까지가 몇 개 있나를 알아보는 것이다.
예를들어 5 -> 16 -> 8 -> 4 -> 2 -> 1 에서는 5, 1, 8, 4, 2, 1 이다. 16이 1로 시작하니까 1로 바꿨다.
모든 숫자들에 대해 그 개수를 세는 것이다. 5의 경우 1이 2개, 2가 하나, 4가 하나... 이런식이다.
수열을 집어넣으면 전부 분해해서 숫자 개수를 적어주는 num_ext를 만들었다.
def num_ext(lists):
numbers = {'1' : 0, '2' : 0, '3' : 0, '4' : 0, '5' : 0, '6' : 0, '7' : 0, '8' : 0, '9' : 0}
for num in lists:
for single in str(num):
numbers[str(int(single))] += 1
break
return numbers
위 함수에 앞서 만들었던 pool 을 이용하여 1부터 100만까지의 콜라츠 수열에 대해 숫자를 전부 쪼개서 개수를 센다.
all_numbers = pool.map(num_ext, [lists for lists in df['series']])
pd_ed = pd.DataFrame(all_numbers)
all_sum = pd_ed.sum().sum()
plt.bar(x=[i+1 for i in range(9)], height=(pd_ed / all_sum).sum())
그러니까 100만개의 작업들을 32개로 그룹지어서 컴퓨터에게 한 덩어리씩 준 것이다.
일꾼이 12마리 명? 이므로 일이 32개니까 농땡이 부릴 여유따윈 없다.
그 근거로 CPU 점유율 100%를 항상 유지하는 것을 알 수 있지 않나.
메모리를 더 사용하게 하고자 한다면 100만이 아니라 10억쯤 하면 된다.
왼쪽은 1 부터 9 까지의 숫자의 개수를 비율로 막대그래프 해서 나타낸 것이다.
FM대로 하면 히스토그램에 막대기 9개로 시각화해야 맞지만 이 코드로 돈 벌게 아니므로 쉽게 가자.
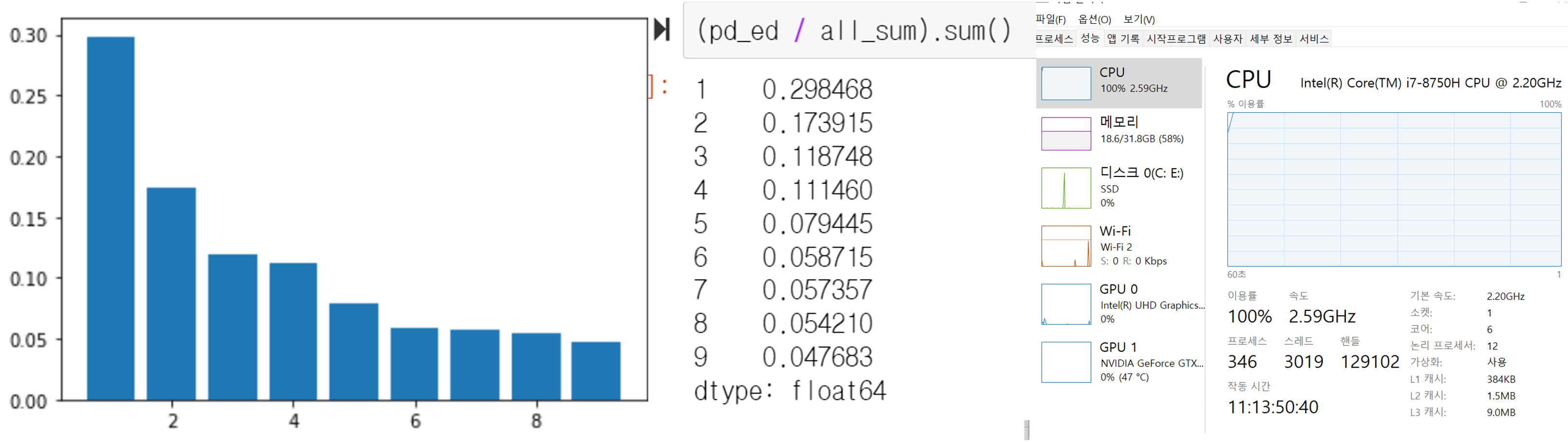
'양극화' 또는 '80대 20 법칙' 아니면 '파레토 분포', '벤포드 법칙' 등등.. 으로 퉁 쳐서 부르는 분포가 나타난다.
예컨데 1, 2, 3 을 다 합치면 59%로 과반수가 넘어가고 7, 8, 9 는 다 합치면 16%로 전체의 일부가 된다.
1이 30퍼센트 정도이고 9가 4퍼센트 정도이니 1에 속한 경우가 9에 속한 경우보다 대충 6.몇배 더 많다.
이러한 경향은 자연상태나 사회구조에서도 나타나는데
아래 표와 같이 소득격차를 나타내는 5분위배율이 대표적인 예시이다.
소득순으로 줄세우고 20%씩 5등분하여 5개의 그룹으로 나누어서
돈을 가장 못 버는 그룹과 가장 잘 버는 그룹의 소득격차를 그 비율로서 나타낸 것이다.

멀리 갈 것 없이 19년 ~ 21년 1분기(그 이후 데이터는 구하지 못함)만 봐도 다 더하여 평균내면 대충 6.몇배가 된다.
이러한 경향은 정도의 차이만 있을 뿐 여기 저기 어디에나 있다.
어느나라건 간에 주식시장에서 상위 몇 개의 일부 대기업이 전체 시총의 과반수 이상을 차지하고
우리나라 세금구조상 과반수 정도의 국민은 소득세를 내지 않으며 일부 부자들이 나라의 세금을 대부분 부담한다.
인터넷 사용자 중 대다수는 댓글을 거의 달지 않고, 댓글을 많이 다는 사람은 극히 일부에 해당한다.
연애시장에서 외모 상위 몇%가 총 연애 횟수의 대다수를 차지한다.
회사에서는 일부 돈을 만드는 직원과 똥을 만드는 나머지 직원이 따로 있다.
데이터사이언스는 100인분의 슈퍼스타가 존재하는 동네다.
수학을 깊게 판 분들 얘기 들어보면 이런식으로 갑자기 분위기 철학이 되는것들이 있다고 한다.
이론물리학 교수님이 슈뢰딩거의 고양이와 고백에 대한 말을 했는데 어떠한 인생을 살아오신 겁니까 교수님...
아무튼간에
지금 예시로 사용한 컴퓨터는 오래된 친구이고, 요즘엔 노트북으로도 32스레드니 64스레드니 있을 것이기에
이 기술을 익힌다면 최소한 열배는 더 빠른 속도를 체감할 수 있을 것이다.
'[중급] 가볍게 이것저것' 카테고리의 다른 글
| 데이터로 알아보는 코로나를 대표하는 키워드! (0) | 2020.04.02 |
|---|---|
| 비트코인 알고리즘 직접 구현해보기 (0) | 2020.04.02 |
| 월마트 맥주와 기저귀 썰에 대한 부분. (0) | 2020.03.25 |
| [R]소득수준 / 소비수준 / 나이 / 성별을 기반으로 고객군 군집화 분석 예제 (0) | 2019.11.11 |
| 고객 장바구니 분석 level_2 (0) | 2019.11.10 |
